Vakar vienas pusprotis mano straipsnyje apie Būlio algebrą parašė komentarą apie tai, kad matematika (tiksliau, visiškai elementarūs skaičiavimai) yra šyvos kumelės briedas. Esmė tame, kad anas komentatorius net esuprato, ką jis skaičiuoja ir jam pasirodė, kad jei prie teigiamų n ir m pridėsi po teigiamą x, tai skirtumas tarp n ir m padidės.
Šiu atveju, kaip supratau, kalba net nebuvo apie aritmetinį skirtumą (vis dar darau prielaidą, kad tokio absurdiško durnumo žmonių čia pas mane neateina). Aritmetinis skirtumas išvis nesikeičia prie tokių sumavimų: (n-m)=(n+x)-(m+x), t.y., koks bebūtų x, jisai nepasikeis.
Kaip supratau, ano komentatoriaus nesuvokimas buvo apie tai, kad jei prie n ir m pridėsim po x, tai pasikeis santykis – t.y., jei n buvo mažiau už m, tai n pasidarys dar mažiau už m. Čia irgi absurdas, tiktai gal ne toks akivaizdus. Absurdiškumas pasimato tada, kai pabandai įsivaizduoti, kaip keisis santykis, keičiantis pajamoms. Gražiausiai tai matosi grafike:
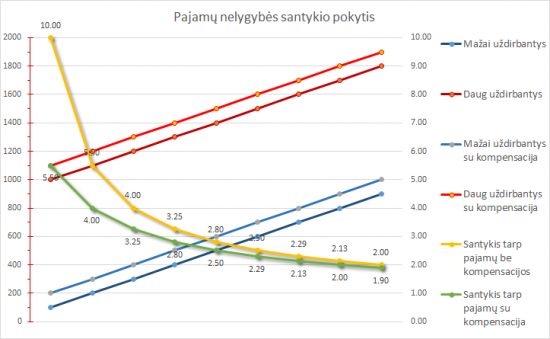
Kaip matome, kuo mažesnės pajamos, tuo labiau pasijunta kompensacijos dydis. Jei pajamos tėra 100 eurų, tai pridėjus 100 eurų kompensaciją ir 100, ir 1000 eurų uždirbantiems, pajamų nelygybė sumažėja kone du kartus – santykis pasikeičia iš 10 į 5,5.
Labai paprasta viską pamatyti, kai pabandai paskaičiuoti: vat tarkim, pas kažką gal pajamos 300 eurų ir valstybė, pvz., apmoka 100 eurų kainuojantį darželį. O pas kažką pajamos gal 1200 eurų, ir valstybė irgi duoda 100 eurų kompensacijos. Kaip pasikeičia santykis tarp pajamų? Ogi be kompensacijos tas santykis buvo 4 kartai, o su kompensacija pasidarė 3,25 karto, t.y., labai labai riebiai sumažėjo.
Aš suprantu, kur kažkam kirmėlės graužia – norisi, kad tie buržujai turčiai negautų jokių kompensacijų, nes jie ir taip turtingi. Bet reikalas tame, kad tiesiniai kompensavimo mechanizmai realiai suveikia kaip progresiniai. Ir net jei neduosi tam daug uždirbančiam kompensacijos, skirtumas pasikeis gana nežymiai: vietoje 3,25 karto bus tiesiog 3 kartai.
Tokie dalykai labai aiškiai pasimato, kai tiesiog pradedi skaičiuoti – nes matematika yra matematika ir viskas. Bet kol nebandai skaičiuoti, tai gaunasi visokie marazmai. O kai į matematiką žiūri kaip ožys į naujus vartus, tai pamatęs tokius skaičiavimus, gali nutarti, kad šitie skaičiavimai yra kažkoks šyvos kumelės briedas.
Deja, čia ne skaičiavimai yra briedas. Durniai yra tik tie, kurie pamatę akivaizdžius skaičius, ima sakyti, kad čia yra nesąmonės.
Beje, aš laikas nuo laiko vis atsimenu, kaip kartą prie straipsnio apie Ebolą ir jos plitimo tempus (tuo metu jie buvo nevaldomi) pas mane atėjo kažkokie humanitarai, kurie, kaip paskui paaiškėjo, net nesugebėjo sudėties nuo daugybos atskirti. Anie puskvaišiai dar paskui man mėtė kažkokias absurdiškas nuorodas, kurias rado, į Google įvedę kažkokius jiems patiems nesuprantamus žodžius. Tomis nuorodomis (nieko bendro netgi neturėjusiomis su tuo, ką jie bandė įrodinėti) jie man bandė įrodyti, kad eksponentinės sekos yra tiesinės 😀
Ponai ir ponios, netgi klaikiai nuobodi matematika būna labai labai įdomi. Bet jei tos klaikiai nuobodžios matematikos pagrindų nesimokai – paskui lieki durniaus vietoje, ir tada iš tavęs kas nors skaldo bajerius, o tu piktiniesi ir nesupranti, kodėl tave durniumi vadina.
Kiek nukrypstant – matematika yra labai įdomi, bet tai, kaip jos moko mokyklose – tai yra klaiku ir pasibaisėtina. Matematikos moko taip, kad ji būna baisesnė gal netgi ir už chemiją. Ir visai nenuostabu, kad beveik niekas jos neišmoksta, o tiktai iškala atmintinai.
Išties matematikos pagrindai nėra sudėtingi, jie yra netgi labai įdomūs ir naudingi, svarbu tik juos suprasti.
Rokiškis Rabinovičius rašo jūsų džiaugsmui
Aš esu jūsų numylėtas ir garbinamas žiurkėnas. Mano pagrindinis blogas - Rokiškis Rabinovičius. Galite mane susirasti ir ant kokio Google Plus, kur aš irgi esu Rokiškis Rabinovičius+.
- Web |
- Google+ |
- More Posts (1489)



Tai jau tikrai… mokyklse nemoko atskleisti, kokia matematika yra naudinga ir graži.
Visi įsivaizduoja, kad tai sausas ir niekam nereikalingas mokslas.
Net įžymusis Davinčis tapė naudojant matematines Fabijačio sekas.
Ne nu jo, bet, bičas. Viskas gerai tekste, bet ašių pavadinimus grafike tai reikia uždėti. Čia kaip elementarus mandagumas, kurio mama turėjo mokyt.
Aš jums uždėsiu: y1 -- pinigai, y2 -- santykis, o tame plote daugybė žmonių.
Buvo juokas, kad ekonomistai yra tie žmonės kurie nemoka matematikos, bet ją daro.
Ai ir buvo toks vienas veikėjas, kuris apsiskaičiavęs, kad BVP pakėlimas nuo 1,5 iki 2,0 procentų gynybai suvalgys papildomai 25 procentus biudžeto.
Nesuprantu as viso sito jusu aukstosios matematikos isvedziojimo. Nesuprantu ne delto kad nezinau kiek bus 2x2, nesuorantu delko reikia isvedZioti. Na gal jei nori koki pgristi koki nors nauja akciza. Arba kompensaciju metodikas.
Juk viskas vyksta daug paprasciau. Pvz: kazkas sugalvojo kazka padaryti savo naudai, na turi jis tolima izvalga. Taigi negali aklai sakyti, karoce ryt bus naujas potvarkis, ir visi jus privalesite vykdyti, nes kitaip mano verslui ar partijos remejams bus blogai.
O siaip tai Lietuvoje veikiai tik viena logika. Sveika konkurencija -- jei vienas pakele kaina, tai konkurentai irgi kartu pakels. Juk negerai issisokti is kitu. Reikia imti kaip ir visi, ne tuoj nurasys kad tu cia kaltas del vissko. Ir tas 100 eur jau buvo, o kuras tai brangsta. Tai paskaciafus infliacijos kooficenta, tai reikia prodeti dar po 50 eur, kad musu visu vaikai galetu eiti pagerintas privacia mokyklas. O jei pas jus kaime nera privacios pagerintos mokyklos, tai jiem neprideti, nes nera kur priedeti. Tada ziurek kiek procentu sutaupusime. O tuos sutaupytus reikia vistiek isleisti, nes nepanaudotus reiks grazinti. Tai vel kaime nera pagerintu mokyklu, tai pridekime dar toms pacioms kur jau turi.
Ir pamatysite, visa Lietuvos svietimo sistema issipres ore.
Ir mano vaikui ir mano vaiok mokyklai bus labai gerai, ir svietimas klestes. Na o jei pas jus kaime nera pagerintos mokyklos, tai patys ir kalti. O mes tai norejome jums paderti, bet jus kaime tai nenotite privaciu pagetontu mokyklu.
O visa sita rasliavai tai pagrysta Bulio teorija ir algebra. Taigi iskas teiseta ir teisinga. Soriukas kad jau taip
Kad vis dar zulinam pavyzdį su darželiais, tai pazulinkime toliau. O šiuo konkrečiu atveju nėra apibrėžta aibė, kurioje kompensacija turi prasmę. Man sunku patikėti, kad kompensacija realiai gali pasinaudoti gaunantys pačias mažiausias pajamas. Nė per kur. Jeigu dar nupaišytume grafikus, kiek lieka lėšų po to, kai pasinaudojama kompensacija, susidarytų kiek kitoks vaizdas. Mano nuomone, ši funkcija neturi prasmės tai pajamų aibei, kai: Pajamos + Kompensacija -- Darželio kaina < Skurdo riba.
Turtingesnėse šalyse buvo analogiškos situacijos su dotacijomis elektromobiliams. Taip, teoriškai, galimybė yra pasinaudoti visiems, bet įvertinus, kad elektromobiliai prasideda gal nuo 30k EUR, na tikrai ne kiekvienam prienaimas skatinimo įrankis.
Ką aš noriu pasakyti: jokiu būdu nesu koks social-komunistas, bet pavyzdys netobulas. Su Petriuko ir Marytės obuoliais būtų žymiai aiškiau. Ir dar: čia išlindo skirtumas tarp grynos matematikos ir ekonomikos su visais socialiniais kintamaisiais.
Toksai variantas, kur kompensacijas praranda skurdieji -- įmanomas, bet su sąlyga, kad nėra valstybinių darželių. Valstybinio darželio suteikimas turi vertę, kuri yra skaičiuojama taip pat, kaip ir kompensacija.
Aš niekur nesakiau kad matematika yra briedas. Briedas yra socialinę nelygybę susiaurinti iki pajamų nelygybės, o pajamų nelygybę supaprastinti iki individų poros pajamų santykio n/m. Tai kad visuomenėje egzistuoja individai su pajamomis n ir m žinoma suponuoja pajamų nelygybę, bet tik tiek.
Šiai individų porai davus po vienodą priedą x pajamų santykis sumažėja, vadinasi kompensacija veikia. Tačiau faktinė situacija Vilniuje su kompensacija už darželius niekaip neatitinka tokio paprasto modelio.
Aš pamėginsiu šį modelį šiek tiek priatinti prie realybės, darydamas prielaidą, kad visuomenę sudaro vieniši individai turintys po vieną ikimokyklinio amžiaus vaiką ir kiekvienas individas gauna mėnesines pajamas. n1 = 500, n2=700, n3=1000, n4 = 4000.
Pajamų pasiskirstymas -- čia mano wild guess klaikiai laisvai interpretuojant Lietuvišką statistiką. Na bet tebūnie, autorius skaičius į grafiką irgi iš lempos surašė.
Paskaičiavus Gini indeksą tokiai visuomenei gauname G=0.375 (palyginimui pasaulio banko estimeitas Lietuvai 2015 m yra 0.374 https://data.worldbank.org/indicator/SI.POV.GINI?locations=LT&view=chart, tad gal visai neblogai ir pataikiau )
1. jei šiai visuomenei išdaliname x=100 priedą, o darželis kainuoja 100 vienam vaikui, tada G=0.348. Taigi pajamų nelygybė ženkliai sumažėja.
2. jei išdaliname x=100, o darželis kainuoja 200, tada gauname G=0.406 (toks indeksas prilygsta Ugandai ir panašioms šalims)
3. jei x=100 paima tik n3 ir n4 ir sumoka uz darželį po 200, tačiau n1 ir n2 paleidžia vaikus į gatvę nes kitaip badas, tada G=0.370.
4. nėra jokių kompensacijų, n1 ir n2 gauna valstybinį daržą, o n3 ir n4 veda vaikus į privatų mokėdami pilną kainą 200, tokiu atveju G=0.356
Įdomiausias variantas yra nr3, nes šios fake visuomenės pajamų nelygybė matematiškai sumažeja nuo 0.375 iki 0.37, tačiau pusė visuomenės negauna ikimokyklinio ugdymo paslaugos, dėl ko socialinė nelygybė gerokai padidėja.
Akivaizdu, kad tikrovė nėra tokia drastiška kaip nr3, bet taip pat nėra ir nr1.
Jūs vat pasėdėjote, pasistengėte su skaičiais, bet jums taip ir nedašilo, kad kai valstybė apmoka už darželį, tai irgi yra kompensavimas -- apmokėjimas. Žodžiu, jūs ir toliau darote labai labai ryškias klaidas. Tai gal tiesiog nedarykit tų klaidų, tokių kaip sugebėjimas nematyti pinigų, ten kur jie yra 😀
Aš suprantu, kad jūs įsivaizduojate, kad darželiai ar jų kompensacijos turėtų veikti kaip progresinio apmokestinimo ekvivalentas, nu bet neturėtų taip būti, kada socialinės paslaugos ar dar kažkas naudojama ne tam, kad paslaugas suteikt, o kad turčius nubaust 😀
Gal čia ne visai į temą,bet kiek man žinoma, UK yra 5 proc. PVM „lengvata“ namų šildymui,dujoms,elektrai (home energy) . O ir maisto produktams PVM berods 0 proc. Irgi visiems,nepriklausomai nuo pajamų.