Neseniai man toksai labai protingas žmogus – ponas Dainius Dzindzalieta, užrodė matematikos egzaminų rezultatus. Buvo pora uždavinių ir rezultatų, kurie išties atskleidžia visą švietimo sistemos ir jos rengiamų programų ydingumą. Netgi ne ydingumą, o kaip čia pasakius tiksliau… Ko gero, visišką išsigimėliškumą.

Egzaminų sistema patiems geriausiams pasako, kad jie esą nevykėliai. Realybė yra tai, kad pati šita egzaminų sistema yra fundamentaliai absurdiška ir vienintelis būdas ją pataisyti – tai banaliai panaikinti iš viso. Jei jūs esate moksleivis, turite gebėjimų ir egzaminas nesigavo – žinokite, kad išties feilinot ne jūs, o tuntas silpnapročių biurokratų, kuurie neturi smegenų.
O paskui dar nuostabiai apie tą švietimo sistemą bei egzaminus parašė ponia Elžbieta Banytė, kuri pastebėjo, kad anei vienas iš tų visai jau rinktinius literatūrinius ir kalbinius gebėjimus bei žinias turinčių moksleivių nepakliuvo į geriausiųjų tarpą – egzaminuose gerus vertinimus gauna kaip tik tie, kas nėra geri. Jos straipsnis apie tai yra puikus.
Bet pradėkim viską nuo pradžių.
Štai pasižiūrėkim, du skirtingi uždaviniai iš matematikos egzamino:
Pirmasis. Išspręskite lygtį: (x-3)(x-7)=21. Išsprendusiųjų – 79,9%.
Antrasis. Supakuotos trys vienodos bandelės kainavo 1 Eur. Pritaikius 40% nuolaidą, vienos bandelės kaina yra… Išsprendusiųjų – 75,4%.
Turint omeny, kad panašių į pirmą uždavinį lygčių sprendimas anei per niekur nei akivaizdus, nei labai gyvenimiškas, nei dar kažkoks, mes galim padaryti vieną labai neišvengiamą prielaidą – ją sprendę mokiniai buvo labiau linkę taikyti standartinius algoritmus, nei analizavimą.
Apie antrą uždavinį kaip tik galim padaryti priešingą prielaidą: su nuolaidomis mums susidurti tenka labai dažnai, tad vienaip ar kitaip įsivertinti ir išspręsti tą uždavinį turėtų būti lengviau. Matematiškai jis irgi daug daug lengvesnis: (1-0,4)/3=x.
Natūralu būtų tikėtis, kad būtent antrą uždavinį išsprendusių moksleivių dalis turėtų būti gana didelė, nes uždavinys paprastas ir įprastas, kaip bepažiūrėsi. O vat pirmo uždavinio išsprendusių dalis turėtų būti daug daug mažesnė. O ką rodo realybė?
Egzaminų realybė rodo, kad paprastą gyvenimišką uždavinį išsprendžia 75,5%, o žymiai sudėtingesnį ir iš esmės sprendimo būdų kalimo reikalaujantį uždavinį išsprendžia 79,9%.
Ką išties tai rodo? Ogi tai, kad dominuoja bukas kalimas, į kurį ir orientuota mokymo programa. Ir tas bukas kalimas yra pakankamai intensyvus ir sistemingas, kad pralenktų netgi visai nedidelio mąstymo reikalaujančių uždavinių rezultatus.
Kalimas savo esme nėra joks mąstymas. Tai yra mąstymo priešingybė: nustatytas kietas algoritmas nepalieka veitos mąstymui, o mąstymas pačia savo esme yra toks, kuris yra platesnis už algoritmą. Netgi beždžionė gali išmokti kokio nors buko algoritmo, tačiau sugalvoti sprendimą ten, kur algoritmo nėra – žymiai sunkiau.
Taigi, klausimas čia tik vienas: ar mes mokome vaikus mąstyti, suprasti ir atrasti sprendimus, ar kaip tik draudžiame mąstyti ir vietoje to verčiame bukai kalti?
Mąstymas esamoje švietimo sistemoje išstumiamas ir naikinamas – tą puikiai pademonstravo jau aukščiau minėta Elžbieta Banytė. Šitie matematinių uždavinių rezultatai irgi demonstruoja būtent tą patį – mokiniai verčiami bukai kalti, o ne mokomi suprasti, kaip vyksta tie skaičiavimai.
O dabar pasižiūrėkime į vieną niuansėlį: reikalas yra tame, kad pagal šitus valstybinius egzaminus paskui reguliuojamas dar ir stojimas į aukštąsias mokyklas. Vietoje to, kad aukštosios mokyklos pasirengtų savo egzaminus, pagal kuriuos atsirinktų tinkamiausius studentus, jos gauna išrūšiuotą mišinį studentų, kur geriausius balus gauna nemąstantys, tuo tarpu kaip tik tie, kas turi geriausius gebėjimus, yra nustumiami į dugną.
Neišvengiamas šitos absurdiškos egzaminų sistemos rezultatas – tai nuolatinė vidutiniausiųjų atranka į geras vietas aukštosiose mokyklose, kartu visiškai diskriminuojant tuos, kas turi gebėjimus ir žinias iš tų sričių, kur jie norėtų stoti.
Tą, beje, rodo ir nuolatinis Egzaminų centro, ar kaip ta įstaiga vadinasi, bandymas kažkaip koreguotis savo egzaminų rezultatus pagal kažkokius nuokrypius nuo standartinio pasiskirstymo. Nors jiems tai nėra akivaizdu (nes jie elementariai to nesuvokia), pati prielaida apie tai, kad rezultatuose turi matytis Gauso kreivė – tai ne kas kita, kaip prielaida, kad žinių lygis yra atsitiktinis. Kitaip tariant, kad moksleivių žinios nukrypsta į gerąją/blogąją pusę ne dėl mokymo kokybės, o tiesiog atsitiktinai. Kad mokymo nėra.
Galime numatyti, kad pvz., mokinių vertinimas grynai pagal batų ir plaukų spalvą irgi duotų pasiskirstymus, kurie būtų artimi Gauso kreivei – kodėl gi pagal tai nepaegzaminuoti? Tikėtina, kad tokio vertinimo rezultatai gerokai primintų egzaminų rezultatus.
Iš tokios Egzaminų centro daromos prielaidos apie esą moksleivių žinioms galiojantį normalųjį pasiskirstymą galima pasidaryti ir išvadą apie tai, kodėl švietimo sistemoje stengiamasi, kad mokiniai bukai kaltų: juk jeigu netiki, kad jie gali mokytis ir išmokti, tai ir telieka bukasis kalimas.
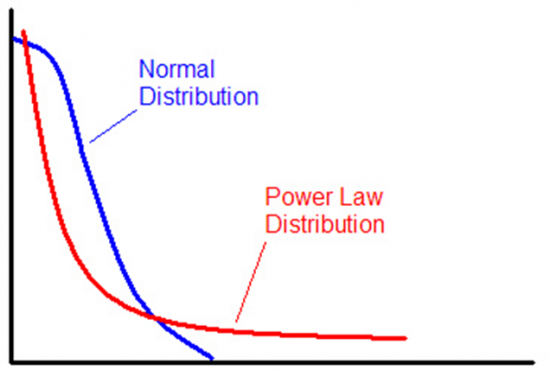
Orientuodamiesi į vidutinybes ir patys būdami visiškomis vidutinybėmis, programų ir egzaminų kūrėjai temato tuos pasiskirstymų segmentus, kurie kreivėse eina paraleliai. Pasižiūrėkite į kreives – mėlynoji atitinka NEC prielaidas apie Gauso pasiskirstymą, kai raudona – Pareto. Šiame paveiksliuke jūs matote matematinę švietimo sistemos absurdiškumo išraišką. Paprastesniems aiškinu paprasčiau: ant vertikalios ašies moksleivių kiekis, ant horizontalios – moksleivių žinios. Raudona kreivė rodo realybę (visur įprastą Pareto principą), o mėlyna – egzaminavimo mechanizmą. Kuo labiau neatitinki egzaminų, tuo blogesnis balas. Atitinkamai, didžiausias žinias ir gebėjimus turintys moksleiviai egzaminų neatitinka labiausiai. BTW, atkreipkit dėmesį į būdingą Pareto kreivės storą uodegą dešinėje – tų gabių moksleivių, kurie gauna blogus egzaminų rezultatus, yra realiai labai daug, nors pačiam egzaminų centrui taip toli gražu neatrodo.
Natūrali prielaida apie žinių skirstymąsi turėtų būti paremta Pareto pasiskirstymu, tačiau šis turi vieną problemėlę: pagal jį kai kurie moksleiviai turėtų būti pripažįstami žinančiais kažkuriuos dalykus geriau ir už mokytojus, ir už egzaminuotojus. Negana to, tektų pripažinti ir tai, kad rinktinius studentus pagal sritis gali atsirinkti tiktai pačios aukštosios mokyklos, bet niekaip ne kažkokia bendravalstybinė egzaminavimo sistema.
Realybė mokyklinių programų ir egzaminavimų sistemoje ne tai kad užmirštama – ji iš principo neigiama. Kaip tik todėl, nuolat bandant menamai gerinti egzaminavimą ir vaizduoti kažkokį biurokratinį teisingumą, įvedama dar daugiau formalių vertinimo kriterijų, kurie dar labiau apriboja bet kokius kūrybiškumo vertinimus. Taip egzaminų tikrintojai ir vertintojai, o ir patys egzaminų kūrėjai vis sako: „čia ne mes kalti, čia aiškūs kriterijai, o tie mokiniai tų kriterijų neatitiko per ten ar ten„. O rezultate dar labiau smunka vertinimo lygis. Ir į aukštąsias dar labiau atrinkinėjami bukesnieji. Ir taip toliau.
Galų gale per tokias atrankas gaunasi dar įdomesnis fenomenas – tokie atrinkti bukesnieji kalikai ilgainiui ir patys tampa mokytojais, ir aukštųjų dėstytojais, ir kokių nors egzaminų rengėjais, ir švietimo programų kūrėjais. Taip užburtas ratas užsidaro. Absurdiška sistema tampa nepataisoma.
Žinote, ką aš jums dar pridėsiu? Ogi tai, kad tikrai atsiras tuntas degeneravusių biurokratų (atitinkančių savo intelektu kairiąją Gauso kreivės dalį), kurie ims sakyti, kad be šitos absurdiškos sistemos negalima, kad ją gal būt dar galima patobulinti ir panašiai, ir dar retoriškai klausinėjančių – „o tai kokias alternatyvas jūs siūlote?„. Na, jūs žinote.
Rokiškis Rabinovičius rašo jūsų džiaugsmui
Aš esu jūsų numylėtas ir garbinamas žiurkėnas. Mano pagrindinis blogas - Rokiškis Rabinovičius. Galite mane susirasti ir ant kokio Google Plus, kur aš irgi esu Rokiškis Rabinovičius+.
- Web |
- Google+ |
- More Posts (1489)



Išlaikęs egzaminus visai neblogai, esu linkęs nesutikti su gerb. Rabinovičiaus rašiniu šia tema. Taip, švietimo sistema formalizuota, orientuota į kalimą ir bevaisė. Tačiau teigti, jog geriausiųjų-blogiausiųjų skalė yra apversta, yra šiek tiek per stipru. Net ne švietimos bėda, kad 25% neišsprendžia paprasčiausio uždavinio su bandele. Jei tesugebi iškalti negyvenimišką uždavinį, tikriausiai ne sistema, o tu pats kaltas. Vargu ar tarp tų kelių procentų, išsprendusių pirmąjį uždavinį ir neišsprendusių antrojo, rasite bent kažką panašaus į kandidatus būti „tarp geriausių“.
Žr. į tą storą Pareto pasiskirstymo galą. Kaip tik jame yra pati esmė: nors toje zonoje, kur abi kreivės yra artimos, egzaminai gali rodyti adekvačius rezultatus, tame gale, kur atsiranda talentai, egzaminai ima rodyti neteisingus rezultatus, nes kriterijai ima neatitikti. Kriterijų neatitikimas tuo didesnis, kuo mokinys protingesnis. Rezultate kaip tik talentai ir nukošiami su prastais egzaminų rezultatais.
Ir bėda čia ne tame, kad 25% neišsprendžia uždavinio su bandele -- tas uždavinys tam tikrai daliai moksleivių išties nėra įkandamas. Gal potencialiai jo neišspręstų 10%, jei mokymas būtų geras, o gal neišspręstų 5% -- ne tame esmė. Esmė yra nuokrypyje, kur formalaus sprendimo reikalaujantis uždavinys sprendžiamas geriau už neišvengiamai minimalaus mąstymo reikalaujantį uždavinį. Ir būtent šitai yra švietimo sistemos bėda.
Beje, tą nukošimo fenomeną jau ne pirmi metai daugelis pastebi, ir kuo toliau, tuo ryškiau -- kai prastai besimokantys mokiniai egzaminuose gauna geresnius rezultatus, negu visokie atitinkamų egzaminų sričių talentai. Čia kaip tik tos storos Pareto uodegos problema.
Laba diena, Rokiški. Kadangi pats kaliau keletui egzaminų (ypač matematikos ir lietuvių rašinio algoritmus), esu gan sugruzintas, kad laikot mane buku, bet ką padarysi. Galbūt jūs ir teisus.
Visiškai sutinku dėl to, kad mokykla moko ir priverčia įtilpti į rėmus (ypač gaila, kai dalykas savaime įdomus ir norisi kuo daugiau sužinoti, bet programa žinančius daugiau žlugdo). Tačiau jeigu nori patekti į aukštąją, tenka pritapti, todėl tampa svarbu palavinti atmintį sukišant tuos algoritmus, ir smagu kai yra mokytojai, bendraujantys su Egzaminų centru bei gebantys išmokyti tų reikalingų algoritmų (dėkui savo lietuvių kalbos mokytojai). Ypač kai tie mokytojai pripažįsta, kad reikalavimai yra idiotiški. 🙂
Visgi, dalį bazinių žinių nesvarbu kaip išmoksi, kalant ar ne, nes supratimas gali ateiti po to. Kai kurių dalykų mokyklos lygmeniu tiesiog neišeina paaiškinti ir turi priimti tai kaip tiesą. Ar elektronų skaičių 2s orbitalėje H atome ramybės būsenoje (0) galima žinoti nekalant? Taip, tiesiog žinai jog H turi 1 elektroną (ar tai iškalimas?) ir principus (irgi kalimas?), kaip pildomos orbitalės. Tačiau tos taisyklės gali būti tiesiog aksiomos, todėl kalimas tampa kaip ir iš dalies reikalingas. Aišku, jūs galite mane nurašyti kaip sistemos išplautų smegenų degradą, bet aš nesutiksiu, jog kalimas nėra galimas mokymosi būdas. Euklidinės geometrijos aksiomos yra intuityvios (pvz. per 2 taškus eina tik viena tiesė), net neįsivaizduoju kaip galima to nesuprasti. Bet kitokiose geometrijose yra kitokios aksiomos, todėl kaip ir būtina šias aksiomas iškalti, jeigu nori suprasti. Regis man daugiau kliūva ta dalis, jog paviršutiniškai klausiant, iškaltos ir suprantamos žinios paprasčiausiai negali būti atskiriamos. O visi egzaminai ir testai valstybiniu mastu yra paviršutiniški.
Klausimas, kiek yra reikalinga žinoti visus pagrindus? Manau jeigu nori būti ekspertas savo srityje turi žinoti pagrindus taip, kad galėtum paprastai paaiškinti. Todėl iš esmės šios žinios aktualios tik mažai daliai žmonių.
Daug rašliavos čia pripyliau, gal neužbaninsi :D.
Supratimas po kalimo paprastai neatsiranda. O jei kažką reikia kalti be supratimo -- tai jau didelis ir kartu labai paprastas klausimas: kodėl?
Aksiomų su taisyklėmis painioti nevertėtų -- aksiomų būna labai nedaug, o visa kita -- teoremos. O vat dėl Euklido geometrijos ir pvz., to paties teiginio, kad per 2 taškus eina tik viena tiesė -- čia dar klausimas, ar aksioma galim laikyti tai, kas intuityviai atrodo akivaizdu. Pasiskaitinėkit kur nors Euklido geometrijos lūžius XIXa. pabaigoje -- XXa. pradžioje, su visais tais aksiomatikų ir teoremų iš serijos „dvi lygiagrečias tieses trečioji kerta tuo pačiu kampu“ reikalais -- nustebsit, kiek ten visko vyko, kol galų gale matematinė metateorija buvo sukurta.
O žiūrint paprasčiau, praktinis faktas yra toks: iškalti dalykai atmintyje neužsilaiko ir supratimo nesukuria. Tuo tarpu supratimas atmintyje užfiksuoja dalykus geriau negu kalimas. Taigi, jeigu tenka kalti, tai vėl tas pats klausimas: kodėl?
Man regis jūs vienas kitą nebūtinai teisingai suprantate 🙂
Yra toks dalykas kaip learning curve: žinios-gebėjimai kreivė. Viskas būtų gerai, jei temos suvokimui reikalingos temos dėliotųsi grynai hierarchiškai ir kreivė būtų sliekas (sigmoidė), bet taip nėra. Norint suvokti temą A, reikia suvokti temas B ir C. Norint suvokti temą B, reikia suvokti A ir C. Ups. Tiesiog paprsatai krūva dalykų yra tarpusavyje visaip susiję ir persipynę ir kol nežinai jų visų apie realų suvokimą nėra net kalbos. Iš čia atsiranda daug plokščių regionų kreivėje.
O bet tačiau didžioji masė besimokančiųjų visgi gavę kokias tai teorines žinias apie vieną ar kitą dalyką/reiškinį jas tuojau pat per kitą ausį išleidžia „bo šito gyvenime vis tiek niekad nepanaudosiu“, nes kur to reikės tiesiog dar nežino. Todėl ypač techninėse specialybėse dažnai susiduriama su „best practices“: įspėjimais apie primėtytus grėblius, kurie padengia didesnę dalį visų situacijų. Ir juos galima taikyti čia ir dabar, suvokimą, kodėl jie egzistuoja ir kada jų nenaudoti perkeliant į vėliau. Tai ir yra tas bukas kalimas.
Čia atsiranda toks kompromisas mokymo kontekste:
a) Mokyti kiekvieną temą izoliuotai su iškalamais naudojimo pavyzdžiais, rizikuojant, kad kreivėje kairiau esantieji nesudės visų taškų ant i ir rezultate teturės paviršutines žinias. Iš esmės temų apjungimo atsakomybė krenta ant mokytojo.
b) Mokyti visas susijusias temas kartu, rizikuojant, kad kreivėje kairiau esantieji pirmiau gautas žinias atmes nes „nafik čia man reikia“ ir liks visiškais degradais, nes ką sujungti į krūvą tiesiog neturės. Taškų ant i sudėjimo atsakomybė krenta ant moksleivių.
a) yra dėkingas esantiems kairėje populiacijos pusėje, b) -- dešinėje. Iš esmės kurį taikyti priklauso kurioje medianos pusėje yra ta kairė/dešinė riba. Spėčiau ties kokiu trečiu kvartiliu. Kadangi taikomas a) galima spėti, kad arba ir ŠMM mano ribą esant virš medianos, arba renkasi lengvesnį variantą 🙂
Kadangi kairiau ribos esančiųjų mokymosi procesą iš esmės diktuoja egzaminai (šito egze nebus, tai nesimokysiu. Šitas egze tesudaro 1% įvertinimo, tai neapsimoka mokytis), tad jie ir formuojami pagal tą patį a) mokymosi procesą. Turbūt su prielaida, kad mokėdamas A, B ir C atskirai moksleivis mokės išspręsti uždavinį reikalaujantį žinių iš visų trijų. Kaip matom taip nėra.
Nereikia išradinėti kažkokių naujų teorijų. Gyvenime yra begalės dalykų su cikliniu žinių reikalavimu. Ir visa tai išsprendžiama labai paprastai -- mokantis minimaliais ir lengviausiai suprantamais gabaliukais, ir tą darant cikliškai, per daug kartų, ir kuo labiau susietai, kad didėtų tikimybė surišti ir paskirus žinių segmentus tarpusavyje, ir vėlgi juos visus su gyvenimiškomis (t.y., supratiminėmis) patirtimis. Ir joks kalimas čia nepadeda -- reikalingas cikliškumas, daugkartinis, su nuolat maksimizuojamu supratimu. Ir kuo daugiau priartinimo prie realybės.
BTW, kompromisai visada reiškia tik vieną -- kad yra pasirenkami blogi variantai, negaunant naudos nei pagal vieną, nei pagal kitą.
Dar dėl kalimo -- yra toks seniai žinomas fenomenas, kurį kadaise pastebėjo socialistinio bloko pedagogai -- mokyklų etape JAV moksleiviai rodo labai prastus rezultatus, lyginant su postsovietiniais, ypač ryškiai tai matosi pradinėse klasėse. Tačiau situacija ima gana juntamai keistis koledžuose, paskui dar labiau aukštosiose mokyklose, o paskutiniuose kursuose gaunasi visiškai priešingai: JAV atsiranda daugybė jaunų mokslininkų, kurie daro begales atradimų, o tuo tarpu sovietinių aukštųjų auklėtiniai beveik nieko nepasiekia.
Visa esmė -- tie patys mokymo metodų skirtumai: JAV mokyklose neverčiama kalti, dėl to didelę dalį laiko mokiniai visur rodo daug prastesnes žinias pagal formalius požymius. Tačiau ten pat labai kreipiamas dėmesys į visko, kas tik įmanoma kvestionavimą, į sąsajas tarp mokomų dalykų ir relybės ir taip toliau. Rezultate, kai jau būdami studentais, žmonės gauna jiems reikalingas žinias, jie neįtikėtinais tempais pereina į realaus mokslo pasaulį, kur pilna kūrybos ir atradimų. Tuo tarpu pagal sovietinę sistemą išdresiruoti kalikai taip ir lieka išdresiruotais kalikais -- jie būna įsisavinę, kad viskas turi būti pagal taisykles ir taškas, o viskas kas nenumatyta -- tai neteisinga. O tai su mokslu nesuderinama.
Prisipažinsiu, perskaičiau iki tos vietos, kur kvadratinės lygties išsprendimas pavadintas „buku kalimu“. Tokiu atveju, 99,99% matematikos yra „bukas kalimas“ 🙂 Todėl ir neskaičiau toliau -- jeigu žmogus mano, kad matematika -- tai bukas kalimas ir kad iš tikrųjų kūrybingi yra tie, kurie jos nesupranta, ir kad mokyklą baigiančiam kūrybingam abiturientui užtenka mokėti trečios klasės aritmetikos veiksmus pritaikyti bulkutės kainai „apskaičiuoti“, tai ką čia beskaityti.
Noriu pasakyti, kad tiems, kas sugeba pertvarkyti pirmąją lygtį į kvadratinę ir ją išspręsti, antrojo kūrybingojo uždavinio spręsti net nereikėtų -- nespėtų pradėti spręsti, atsakymas jiems būtų akivaizdus be jokio sprendimo! Sprendimo apiforminimą tektų sugalvoti truputį vėliau -- nes juk nepateiksi pliko rezultato.
Gal ten straipsnyje toliau yra protingesnių minčių, bet iki tos vietos, kiek perskaičiau, man pasirodė, kad autorius propaguoja idiotukų „kūtybiškumą“, kai mokyklą baigęs abiturientas tesugeba ką nors pagūglinti. Tenka su tokiais susidurti darbe. Elementariausios užduotys, kurias normalus žmogus atlieka per pusdienį, jiems -- tarsi diplominio rašymas, be poros savaičių niekaip.
Gal būtų galima sužinoti, kokios tai užduotys? Ačiū
Mokyklose mokomas kvadratinės lygties sprendimo algoritmas yra paremtas diskriminantu, kuris tikrai nėra nei elementarus, nei intuityvus savo esme, o tik tiek kad lengvai iškalamas. Tiesą sakant, intuityvumo požiūriu visokias matricas yra žymiai paprasčiau ir suprasti, ir spręsti. Tačiau vat norint iškalti bukai -- diskriminantas daug lengvesnis. Nereikia tada galvoti, kodėl jis toks ir koks jo sąryšis su visa ta lygtimi ir ką jis išvis rodo.
Ar nebus tamstai paprsčiau visgi iškalti ką nors atmintinai, negu pagalvoti, kas ir kaip ir kodėl? Gal išties paprssčiau neskaityti, negalvoti, o išsyk turėti tam tikrą iš anksto suformuotą nuomonę? 😀
Rašei ,,Kas sugeba pertvarkyti pirmąją lygtį į kvadratinę ir ją išspręsti, antrojo kūrybingojo uždavinio spręsti net nereikėtų — nespėtų pradėti spręsti, atsakymas jiems būtų akivaizdus be jokio sprendimo! Sprendimo apiforminimą tektų sugalvoti truputį vėliau — nes juk nepateiksi pliko rezultato.“
Dar kartą perskaityk tai ir pamąstyk: tai kodėl vis dėl to antrą uždavinį išprendė 5.4% mažiau abiturientų nei pirmą?
Gal antrojo uždavinio ,,atsakymas būtų toks akivaizdus“ kad jie net nesivargino jo spręsti? Ar vis dėl to tie 5.4% sugebėjo ,,pertvarkyti pirmąją lygtį į kvadratinę ir ją išspręsti“, bet ,,antrojo kūrybingojo uždavinio“ nesugebėjo? Ir ar tai ne švietimo sistemos klaida?
Problema ne tame, kad švietimas moko KALTI, o tame, kad moko TIK KALTI.
ksiačiau pradžią, nuoširdžiai tikėdamas, kad čia ironija ir kad _any minute now_ bus normalus paaiškinimas kas po kam. Pasirodo ne. Visas postas kažkokia parodija. Taip ir likau nesupratęs kokie čia tikslai buvo siekiami.
p.s. Gauso pasiskirstymo kreivė šiaip jau atrodo kitaip nei jūsų diagramoje. https://lt.wikipedia.org/wiki/Normalusis_skirstinys Tad vėlgi, likau nesupratęs ką lyg ir protingas žmogus čia išdarinėja.
p.p.s praeičiau pro šalį, bet tema jautri, nesusilaikiau. Jaunimo rezultatai nedžiugina, bet jei deja daugmaž atitinka tą realybę su kuria kartais susiduriu. FB ir instagramo karta jmj.
Aha, visa Gauso kreivė atrodo kitaip. Nes čia jos pusė. Pusės atpažinti nesigauna, ar ne? 😀
Ponas Rokiški, jūsų straipsniui buvo suskaičiuotas diskriminantas.
Čia, manau, kiek klaidina ir pasirinktas Gauso kreivės atvaizdavimas, kuris nulį turėtų pasiekti tik riboje, o ne taip, kaip dabar pavaizduota grafike. Taip pat, išsakyta mintis, jog Pareto skirstinys teoriškai leidžia egzistuoti mokiniams, žinantiems geriau už mokytojus, iš tiesų galioja ir Gauso pasiskirstymui (nors ir gerokai mažesne apimtimi). Kadangi apie tai nėra užsiminta, natūraliai atrodo, jog rašyta būtent apie skirstinį grafike, o ne Gauso.
Šiaip cummulative Gaussian function, o ne pusė ten turi būti (kuri panaši ir esmės nekeičia).
Bet kodėl manote, kad paretas čia teisingas apibrėžimas?
Labai elementaru: jei žmogus mokosi ir gauna žinias, jam lengviau mokytis toliau ir daugiau. Todėl tie, kuriems įdomu, kurie domisi kažkuria sritimi, žinias gauna žymiai gilesnes ir platesnes. Atitinkamai, jiems mokytis darosi dar lengviau ir įdomiau. Todėl pasiskirstymas gaunasi su labai dideliu nuokrypiu į tai, kad mažumos galvose būtų didžioji dalis žinių.
Paprastai kalbant, tie mokiniai, kurie yra idėjiniai moksliukai, žino ir moka labai labai daug. Ir tokiu būdu kokie 80% žinių atsiduria kokiose 20% galvų. O tuo tarpu likę 80% galvų teturi kokias 20% žinių. Tai yra natūralus procesas, kurio ir verta tikėtis. Tas pat, kaip ir ekonomikoje, su pinigų pasiskirstymu.
Priešingas požiūris, kad žinios skirstosi pagal Gauso pasiskirstymą, gali remtis tik prielaida, kad nėra jokio savarankiško mokymosi ir gilinimosi į kažkokią sritį, o tos žinios tiesiog tikimybiškai užsifiksuoja tikimybinėse galvose, esančiose standartiškose mokyklų klasėse. Ir viskas.
Iš esmės, tam tikru kampu žiūrint, abu požiūriai gali galioti realybėje. Pagal egzaminų rezultatų situaciją panašu, kad esame kažkur gana netoli nuo antrojo modelio. O tuos, kas neatitinka to modelio, per daug mąsto ir gilinasi, mokosi daugiau, nei numatyta mokyklos kurse -- tiesiog išbrokuojame. Nes tiesiog jie to modelio neatitinka. Vat ir viskas.
Nepykit, čia bus šiek tiek minčių kratinys.
1. Ar tikrai „bukas kalimas“ yra taip blogai? Įdomumo vardan galėtumėt padaryti tos pačios matematikos programos analizę ir įvertinti, kiek gi ten punktų reikia iškalti. Kiek dar atmintis traukia, tikrai nebuvo nesuvokiami informacijos kalnai.
2. Nepavyko dorai išlaikyti egzaminų? Ne bėda! Kartelė į aukštąsias yra taip žemai, kad visi gabūs „nevidutinybės“ ten įstos be didesnių problemų.
3. Sakyčiau, kad didesnės problemos yra su konkursinio balo skaičiavimu, kai per lietuvių kalbą žmogus gali nepatekti į tiksliųjų mokslų studijas(nors vėlgi, dėl 2 punkto, unlikely).
4. Reiktų kalbėti apie mokyklų darbo kokybę, jei mokiniai išties nėra kokybiškai paruošiami standartizuotam testui.
5. Tikslios informacijos nežinau, bet spėju, kad egzaminų rezultatai daugiau mažiau koreliuoja su tuo, ar moksleivis lankė pamokas, ar dažniau gėrė miškelyje už mokyklos. Greičiausiai rezultatai aukštojoje -- taip pat.
6. Visiškai neneigiu kritikos lietuvių k. egzaminui -- dažnai atsiduoda loterija.
7. Dėl alternatyvų tai galėtumėt ir apšviesti, kaip, pvz., daro suomiai?
Apskritai, pritariu Burgio ir Jurkevičiaus pozicijoms -- turbūt yra vienetai, kurie nepateko į aukštąsias dėl blogos sistemos, o ne dėl to, kad tingėjo mokytis.
Vel atrandama, kad svietimo sistema kuria tik papugos-triusio hybridus. Papugos gali kartoti ka girdejo, o kiskis bijo visko. O dabar isivaizduokime kokia yra tikimybe, kad svietimo sistemos atrinkti mokytojai (papugos-triusiai) gali ka nors pakeisti? Del papugos komplekso yra tiesiog neigalus, nes nieko naujo nesugalvos. O del triusio komplekso tikrai nedris ka nors keisti.
Kaip tik esu abiturientas gavęs itin gerus egzaminų rezultatus -- porą šimtukų, o likę >90 😀 Sutinku, kad vertinimo sistema yra absurdiška -- ypač lietuvių su tom formaliom lentelėm, kur išvardinti visi galimi argumentai. Arba biologija -- užduotyje abstrakčiai prašoma paaiškinti fermentų veikimo principą, tačiau kažkodėl netinka aiškinimas, kaip fermentas susijugia su substratu ir pan., tiesiog aklai iešoma dviejų raktinių frazių -- pagreitina reakciją, sumažina aktyvacijos energiją. Vis dėlto nesutinku su pora jūsų straipsnyje minimų dalykų -- visų pirma matematikos programai jokių priekaištų neturiu. Pateiktoje lygtyje kaip tik prašoma ne pritaikyti standartinį kvadratinės lygties algoritmą, o sumąstyti, kaip reikėtų lygtį pertvarkyti, nes tai nėra visiškai akivaizdu (atskliausti, sutraukti narius į vieną pusę). Antram uždaviniui su bandėlėmis kaip tik algoritmas yra daug akivaizdesnis (apskaičiuoti kainą po nuolaidos ir padalinti iš 3), tačiau dauguma tiesiog iš žioplumo kaip atsakymą paliko trijų bandelių kainą. Ir kitas jūsų teiginys, kad egzaminus gerai išlaiko tik vidutinybės irgi truputį prasilenkia su tikrove (su retomis išimtimis), nes visokie būsimi chickenfactory emigrantai kaip taisyklė egzaminus vos išlaiko, o gudrūs mokiniai įstojantys į visokius Oksfordus, vis tiek supranta, kad egzamine reikia viską rašyti „pagal normas“ ir gauna labai gerus įvertinimus, taigi teigti kad visiškai jokio mokinių išrūšiavimo egzaminas nedaro, negalima.
Aha, su tais paskutiniais problema taip pat yra. Mano mama mokytoja, tai dažnai papasakoja apie savo mokinius, Buvo labai negabių, ta prasme, kur tikrai galvoji, kad neišlaikys egzamino, nes rašo nesvuokiamas nęsamones, bet sugebėjo surinkti virš 30%. Dėl išdėstytų autorius minčių sutinku, nes tech startupuose ir pan. Dažniausiai visi klausinėj dėl karjėros galimybių bet tokių kurie ką nors norėtu kurti arba sugalvotų naujas įdėjas ta prasme, tikrai reikalingas, tokių vis mažiau atsiranda.
O iš tikro, gerbiamas žiurkėne, ką mes galim padaryt prieš biurokratinį aparatą? Aš pats esu viena koja mokytojas, bet atrodo teks atsisakyti šito prabangaus užsiėmimo, nes tikrai velniškai sunku yra suteikt kokybišką išsilavinimą jaunam žmogui, jeigu dirbi su daugiau nei trimis vienu metu. Kol yra individualus darbas, dar galima ir save išlankstyt ir prie to jauno žmogaus proto vingių prisiderint, juos suprast ir pratęst. Kai prasideda statistika-masė, jau vyksta chaosas…
Vienok vistiek nepateisinu tokios egzaminavimo sistemos, kokią turime dabar. Tačiau sistema kaip sniego kamuolys -- kas bus ta stabdanti siena?
Neklausiu, ką dar galima pasiūlyti. Klausiu, KAIP kažką naujo pasiūlyti?
Baigiau mokykla pries 3 metus ir net nebeatsimenu diskriminanto formules… Taciau sitame uzdavinyje to netgi nereikejo. Man kaip tik atrode, kad tas pirmas uzdavinys yra labai praktiskas, kadangi jis patikrina kaip moksleivis sugeba pasirinkti trumpesni kelia arba kaip subega issisukti is sudetingos padeties paprascau -- kas labai reikalinga gyvenime. Klausime buvo pateikti atsakymo variantai ir tereikejo isistatyti pateiktas reiksmes ir patikrinti lygybe. Ir siaip, paziurejus i pateiktus atsakymo variantus is karto gali suprasti, kuris atsakymas yra teisingas… „A) 3 ir 7“ -- abu skaiciai duoda atsakyma 0, „B) 0 ir 10“ -- abu skaiciai duoda atsakyma 21, „C) 10“ duoda 10, taciau vienas skrendinys lieka neatrastas bei „D) sprendiniu nera“ -- tiesiog negaleju buti, jeigu pabandei isistatyti B bei C reiksmes. O ir be atsakymo variantu buvo labai paprasta atsakyma tiesiog atspeti, kadangi pateikta forma yra jau suskliausta. Nesu uz sia mosklo sistema, taciau matematika nera kalimas, matematika yra priesingai, supratimas.
Dauguma to diskriminanto neatsimena jau praėjus metams-dviems po mokyklos baigimo. Iškaltas daiktas ilgai galvoje neišsilaiko.
O dėl spėliojimo -- aš nemanau, kad egzaminavimas turėtų būti skirtas mokinių spėliojimo gebėjimams patikrinti. Jei tikrinamas spėliojimo gebėjimas, tai tada ir pats egzaminavimas pavirsta į tikimybinį. Kas, beje, reikia pripažinti, atitiktų NEC koncepcijas. Jie kaip tik ir įsivaizduoja, kad visos žinios tikimybinės.
Taigi, paradoksalu, tačiau tamsta gal netgi taikliau už mane pataikėte -- gali būti, jog išties egzamino sisteminė (gal net pačių kūrėjų nelabai suvokiama) esmė yra ne patikrinti žinias, o padalinti balus tikimybiškai. Ir tada visi galai sueina, ir metodiškai irgi. Ir Gauso kreivė turi gautis. Njo…
Šiaip jo, padarius tikimybinį pataikymą, visi galai išties susieina su tais egzaminais. Ir tai netgi paaiškina, kodėl jie tiki tuo visu savo kliedesišku absurdu -- jie tiesiog tiki, kad tikimybės pas geriau pasiruošusius bus didesnės. Ir jie tuo paaiškina viską ir nesigilina. O tie moksleiviai, kurie per daug mąsto -- feilina, nes nežaidžia tikimybiškais pataikymais, atitinkamai, nukrypsta ir viskas -- nesurenka pataikymų.
Jei išties taip, tai dar žiauriau nei galėjau pagalvoti. Matyt trūksta man visgi cinizmo. Pernelyg esu linkęs tikėti tuo, kad net ir tokiose kontorose žmonės kartais turi smegenų.
Taip, matyt visgi tamsta teisus. Sukėlėt čia man minčių.
Jei, kaip rašote, lygties galimi atsakymai pateikti, tai uždavinys netikrina ar moksleivis moka spręsti kvadratinę lygtį, uždavinys tikrina, ar moka įstatyti duotus skaičius į reiškinį. Tai paaiškina, kodėl bandelių uždavinį buvo sunkiau išspręsti -- jame iš tikro reikėjo _sugalvoti_ kaip spręsti, idant galėtum parinkti teisingą atsakymą.
lmn mane suprato 😀 O siaip, bandeliu uzdavinys taip pat turejo pateiktus atsakymo variantus, tiesiog reikejo sugalvoti sprendima ir ji pasitikrinti, nes galimi atsakymo variantai jau duoti. Ponas autorius, deja, manes nesuprato… Norejau pasakyti, kad uzdavinys tikrina gebejima galvoti, o ne naudoti iskalta sprendimo buda. Tie, kurie naudojo diskriminanta, nesupranto uzdavinio esmes, nes tikriausiai sugaiso daug daugiau laiko spresdami, nei tie, kurie tiesiog zvilgtelejo i atsakymo variantus. Beje, tas pats yra ir gyvenime… Gali pasirinkti eiti sunkiu ir ilgu keliu arba pamatysi trumpesni kelia ir juo pasinaudoti.. 😀
Tai kad kvadratinės lygties šaknų formulė, kaip ir visos kitos -- pateikta. O Lietuvoje ką nors suprantančių reikia labai mažai, pakanka baigti vadybą, administravimą, turėti ryšių ir iki pensijos vldysi valstybę.
Nuo kada lygčiai su vienu kintamuoju išspręsti reikia dviejų sprendinių?
Ai, supratau, čia du galimi sprendiniai. Matyt jau ir pats matematiką baigiu užmiršti… 🙂
Nenuvertinčiau to bandelių uždavinio. Dalis moksleivių visiškai nejaučia ryšio tarp matematikos ir realaus pasaulio, todėl susiformuluoti ir išspręsti net elementarų uždavinį iškyla problema. Bandelių uždavinys ta prasme ir sunkesnis, kad jame matematinę išraišką reikia susiformuluoti pačiam. Tai padaryti gali tapti dar sunkiau, jei staiga pajunti alkį, burnoje pradeda kauptis seilės, o vaizduotė užsipildo kvapniomis minkštomis bandelėmis, ir dar su nuolaida…
Kitas reikalas -- egzaminai orientuojami į vidutinybes, man atrodo to niekas neslepia, galbūt kitaip ir neturi būti. Turintiems realių gabumų matematikai, į vidutinybes orientuotas egzaminas nėra tinkamas atskleisti visą savo talentą ir gabumus, adekvačiai išsiskirti iš vidutinybių, ir nesu tikras, ar įmanoma valstybinį egzaminą padaryti tam tinkamą -- tokiam reikalui reikia ieškoti kitų platformų. Bent mano laikais stojamojoje srityje pademonstravę išskirtinius rezultatus (valstybinių ar tarptautinių olimpiadų laureatai, sporto turnyrų nugalėtojai ir pan.) gaudavo papildomus stojamuosius balus. Aišku, taip gali atsisijoti vienetai, bet apskritai gyvenime iššvaistoma daug talento, ir tikrai ne valstybiniai egzaminai yra pagrindinė to priežastis.
Būtent todėl, kad tas bandelių uždavinys yra apie realų pasaulį -- būtent todėl jis ir rodo, kad moksleiviai dažnai nesuvokia koks ryšys tarp to, ką jie kala atmintinai ir tiesiog realaus pasaulio. Ir būtent šitai yra visiškai tiesioginis ir vienareikšmis požymis, kad mokymas yra prastas, paremtas kalimu, o ne supratimu. Taip neturi būti.
Jei paprastesni, bet gyvenimiški (t.y., supratimo reikalaujantys) uždaviniai nesuprantami, o tuo tarpu geriau išmokstami nesuprantami -- tai vienareikšmiškai rodo, kad žinios išties netampa žiniomis. Čia gaunasi panašiai, lyg mokiniai atmintinai kaltų kažkokias mantras nesuprantama kalba ir paskui pagal tai būtų egzaminuojami -- tai absurdas.
Niekaip nesuprantu kodėl gabus mokinys negalėtų prisitaikyti prie egzaminų vertinimo reikalavimų? Jei jis to nesugeba, tingi ar nesuvokia poreikio, tai gal egzaminai kaip tik puikiai atlieka savo darbą ir nuleidžia ant žemės tokius „pasimetusius“?
Kažkas jau komentavo, bet pasikartosiu -- egzaminų rezultatų reikia tik įstojimui. Maksimalus rezultatas tinka pasipuikavimui ir šiaip malonu, bet nelabai kam daugiau reikalingas (pataisykit jei klystu). Taigi net jei kažkaip netinkamai įvertinam ypač gabius -- kur bėda?
Taigi, ar jūs sakote, kad jei yra daromas absurdas (nesąmoningas egzaminavimas), tai mokiniai turėtų prisitaikyti prie to absurdo ir jei jie nesugeba atitikti absurdo kriterijų, tai reiškia, kad problema ne absurde, o mokiniuose. Aš suprantu, ką norite pasakyti.
Laba diena. Stojamieji. Lyg ne pas jus būčiau puikiausius straipsnius apie sovietizmo debiliškumus skaitęs.
Stojamųjų atsisakyta buvo, nes kol buvo ši sistema pareidavo vertintojams kiekviename egze lapukas su jau iš anksto „praėjusiais“—dekano sūnėnais, prorektoriaus dukromis ir t.t. Šiais laikais valstybinį egzaminą nusipirkti yra nepalyginamai sunkiau ir brangiau. Jokių stojamųjų LT. Ir niekur kiek dabar atsimenu (Vokietija, JK, Amerika) stojamųjų nėra. Į bakalaurą. Magistre irgi dažniausiai ne, į doktorantūrą pokalbis yra.
Dzindzalieta šaunuolis, kad stengiasi, bet jo 8-okų raportą sugebėjau perskaityti iki pirmo puslapio vidurio, kol nepradėjau piktintis jo piktinimusi. Juokas iš to raporto paėmė tiek man, tiek tėvui (inžienierius), tiek močiutei (mt mokytoja, pensijoj).
Taip, čia tesingiai sakote apie tą stojamųjų sistemą, kuri tais laikais veikė. Viena aukštoji anais laikais garsėjo, kaip sugebanti kai kada į visą kursą nepriimti nei vieno, kuris būtų ne per kyšius ir pažintis.
Kitas reikalas, kad šiais laikais situacija keičiasi -- studentai puikiai gali rinktis, kur jiems eiti. Paprašė kyšio -- siunti ant trijų raidžių. Įstoja kyšininkai -- lygis žemas. Bendrai imant, kyšininkavimas per aukštųjų stojamuosius ėmė po truputį byrėti vos pasibaigus sovietmečiui -- kaip tik dėl augančių pasirinkimo galimybių, augančio aukštojo mokslo prieinamumo ir dar dėl vienos priežasties -- dingo tas mechanizmas, kai neįstojusius į aukštąsias siųsdavo į sovietinę armiją.
Kita vertus, faktas ir tas, kad bendra pažymių sistema tiesiog pačia savo esme negali būti adekvati. Vat ir viskas.
Tiesą sakant, aš nežinau gero ir visapusiško sprendimo, kuris būtų idealus. Aš tik matau, kad bandymas kovoti su korupcija per tą standartizavimą pavirto į kažkokį marazmą.
Ir dar. Savo klasei parodyti ir papildomiems balams susirinkti, yra olimpiados, fotonai etc. Aišku motyvacinio laiško įvedimas kaip kad JK yra diskutuotinas. Tada koks jaunasis literatas galėtų pasigirti nuo 15-os rašantis straipsnius į „Artoją“ 🙂
Kita vertus, yra ir vokiška sistema. Visi baigę gimnazijas (kokių 30% berods šiais laikais) priimami. Na neskaitant medicinos, teisės etc. Kur konkursas didelis. Tada po pirmo semestro pusė iškrenta.
Vokietijoje yra trys mokyklų lygiai ir seniau kokių 12-os kaip išskirstydavo, taip ir nebegalėdavai pasikelti. Malei š pradinėj—tebūsi kokiu nors duonkepiu. Todėl po šiai dienai Vokietijoje mažas nedarbas.
https://en.wikipedia.org/wiki/Education_in_Germany#Secondary_education
„Netgi beždžionė gali išmokti kokio nors buko algoritmo, tačiau sugalvoti sprendimą ten, kur algoritmo nėra – žymiai sunkiau.“ -- nagi ir pats sau prieštaraujate. Iš pradžių sakot, kad gyvenimiškas uždavinys lengvesnis, kad jį turėtų išspręsti daugiau moksleivių, o paskui jau sakote kad būtent pirmąjį uždavinį išspręstų ir beždžionė, o antrąjį išspręsti -- kur kas sunkiau. Manau reiktų tiksliai apsvarstyti prieš rašant tokį straipsnį, nes jūsų lūpomis labiau kalba pyktis, o ne pagrįsti ir gerai apgalvoti argumentai. Man asmeniškai ir visiems, ką pažįstu, žodiniai uždaviniai, žinoma, yra daug sunkesni. Lygčių sprendimo niekaip logiškai neišmąstysi, reikia žinoti tam tikrus algoritmus. Niekada tas, kuris nesimoko formulių ir taisyklių, nors ir yra žiauriai proingas, nepasieks geriausių rezultatų, taip pat kaip ir tas, kuris tik kala, bet nieko nesugeba. Čia jau viską nulemia ir žmogaus genai, nulemiantys tam tikrus loginius sugebėjimus.
Ponas, algoritmo vykdymas -- tai yra algoritmo vykdymas ir viskas. Mąstymas, kur nėra algoritmo -- tai savo esme naujo algoritmo sukūrimas (kas suponuoja ir algoritmo sukūrimą, ir vykdymą, kas jau ir kokybiškai ir kiekybiškai sudėtingiau). Pats sprendimas, kai nėra algoritmo -- akivaizdžiai lengvesnis gyvenimiško uždavinio atveju. Tačiau tuo atveju, kai nemąstai, o štai algoritmą vykdai -- tai aišku, kad lengviau su tuo, kur mąstymo nereikia. Ir čia ir pasimato skirtumai.
Šiaip tamsta mąstote teisinga linkme. Tai gal sunku įsikirsti, bet algoritmas atstoja mąstymą. Štai ir viskas.
Taip pat siūlyčiau pasidomėti, ar tokie minimalūs procentiniai skirtumai kaip 75,5 bei 79,9 yra statistiškai reikšmingi, ar tiesiog yra galimi nurašyti atsitiktinei paklaidai
Siuo atveju reiksmingi, nes atskaitos taskas turetu buti ne vienodas isprendusiuju procentas, bet tam tikras skirtumas i visai kita puse, is akies primetant, koks 10-15%.
vadinasi skirtumas nuo normos ne 4.4%, o jau cieli 14-19%.
Tikiuosi suprantamai issireiskiau. Skaiciai is akies, bet esme matyt pagaunat.
Labas Rokiški! Baigiau šiemet dvylika klasių, laikiau 5 egzaminus. Planavau stoti į universitetą, programavimą. Dalyvavau visuose 5-iuose egzaminuose, maniau neblogai pasirodžiau. Atėjo rezultatų viešinimo dienos. Anglų -- išlaikiau garantuotai. Liepos 4 -- po ilgų kančių kuomet neveikė NEC rezultatų viešinimo svetainė, sužinojau, kad matematikos išlaikiau mažesniam balui nei gavau taškų, bet visgi gerai išlaikiau, o štai lietuvių valstybinis NEIŠLAIKYTAS! (iš bandomojo egzamino buvau gavęs 6/10, kurį vertino labai griežta ir principinga mokytoja) Už ką, kodėl?!! Viskas, galas mano karjerai! Negausiu valstybės finansuojamos vietos kur reikia būtinai būt išlaikiusiam VALSTYBINĮ literatūros egzaminą, be to sumažės konkursinis balas…
Kalbant apie valstybinį egzaminą, aš vykdžiau jų reikalavimus, 500 žodžių, į temą, rėmiausi autoriumi… Pripažįstu, esu tiksliukas todėl nesu apsigimęs literatūros kritikos, negalėjau gerai pasirodyti šioje srityje, bet aš tikrai žinau, kad esu raštingas, sugebu mąstyti, analizuoti ir sklandžiai dėstyti mintis (esą NEC tikslas patikrinti ar sugeba mokinys dėstyti savo mintis su visokiais pribumbasias)…
Taigi paskyrė perlaikymo datą -- liepos 7 d. MOKYKLINIS egzaminas. Parašiau tą prakeiktą rašinį „Kam žmogui reikalingi namai“ tema, gal kiek geriau nei praeitą kartą, geresnis autorius pasitaikė šį kart. Laukiu rezultatų.
Kitą dieną paaiškėja kitų dviejų mano egzaminų rezultatai. Informatika 88 -- tiek ir tikėjausi, nes kai ko nepadariau pritrūkus laiko. Istorija 56 (???!!!). Ką, kas antrą atsakymą išbrokavo?! Kas jau kas, bet istoriją išmanau puikiai, turėjau dešimtukus, iš bandomojo egzo buvau 8/10 gavęs. Aišku aš neakcentuoju bandomųjų egzaminų rezultatų ir mokyklinių pažymių, nes daugeliu atveju būna mokytojai pakelia arba sumažina pažymius. Bet aš išimtis, nes mokiausi nuotoliniu būdu, nei aš mokytojų, nei mokytojų nepažinau, bei nesimpatizavo. Peržiūrėjęs teisingus atsakymus ir savo parašytus, supratau, jog čia ne aš kaltas, o bukas vertinimas pagal „lentelėse esančius teisingus teiginius“. Mano teiginiai irgi buvo teisingi, tik jie nebuvo tose „legalizacijos lentelėse“. Jomajo, juk negaliu atspėti kas jų galvoj dedasi, kokių atsakymų jie nori žodis į žodį… Mažų mažiausiai turėjau gauti 76… Taip, buvo šiek tiek kvailų klaidų, bet tai ne dėl nežinojimo, nemąstymo, bukumo. Iškalbingas faktas -- iš 10 tūkst. istorijos laikiusių mokinių tik 7 gavo 100 balų įvertinimą… Kame šuo pakastas, jeigu iš informatikos, 2252 laikiusių net 246 gavo 100 balų įvertinimą? Čia slypi esmė, kad matematikos, informatikos, fizikos, chemijos, dalis užsienio kalbų egzamino atsakymų gali būti tik vienas ir tikslus. O istorijos, ir ypač lietuvių vertinimas labai abstraktus ir vertina tai ką įvertinti visai kitus dalykus. Vertina ar kiekvienas pasakytas teiginys yra tose sušiktose lentelėse (vertinimo instrukcijose). Jeigu nėra, arba vertintojas nesutinka su išsakyta nuomone -- su mielu noru parašys nulį, o po to viešai skųsis, kad negalėjo kitaip vertinti, tik pagal vertinimo kriterijus… Ydinga sistema.
Atėjo atsitiktinė lemiama diena -- liepos 12 sužinojau savo mokylinio perlaikyto literatūros egzamino įvertinimą -- 4 iš 10. Huh, per plauką IŠLAIKIAU! Vadinasi gausiu brandos atestatą ir turėsiu teisę nors už pinigus studijuoti universitete patinkančią specialybę. Per šias dienas, nuo 4 d. iki 12 d. padėjau nemažai nervinių ląstelių -- išlaikysiu ar ne… Juk aš jokio plano B nebuvau sugalvojęs juodžiausio scenarijaus atveju. Tikrai žinojau, kad išlaikysiu valstybinį egzaminą… O kad šitaip nutiktų.. nė košmare nesapnavau. Laimei, pabaiga su „laiminga pabaiga“ -- mokylinis egzaminas išlaikytas, brandos atestatas garantuotas. Toliau žiūrėsiu kaip gausis.
Šios mano istorijos moralas, toks, kad iš vieno rašinio nusprendžia ar gausi studijoms valstybinį finansavimą. Kokia ydinga sistema, koks neadekvatus literatūros (neva lietuvių k. ir literatūros) egzamino ir kitų egzaminų vertinimas, užduočių kūrimas, ir aplamai visa ši vieninga bendra stojimų sistema. Taip gaunasi, kad kokia nors „stropi“ mokinė(ys) labai gerai parašiusi valstybinio egzamino rašinį, gavusi didelį įvertinimą bei vos išlaikiusi kitus egzaminus, nieko nenutuokianti apie pačią specialybę lengvai gali patekti ir gauti valstybės finansavimą, o aš tuo tarpu, nesėkmingai bandžiusiam laimėti valstybinio egzamino bylą prieš lituanistus , su vos per plauką išlaikytu mokykliniu egzaminu netenku teisės gauti finansuojamos vietos, nors galbūt aš jos visai pelnytai nusipelnau, juk apie pačią specialybę nemažai žinau, moku daug daugiau nei patys mokytojai ar vertintojai, iš egzamino taip pat gavau aukštą įvertinimą… Valstybė viena ranka duoda, kita ranka atima. Padidino IT finansuojamų vietų iki 1050, bet net neturiu teisės konkuruoti dėl šios vietos (aš tik teprašau leisti man konkuruoti su turimais konkursiniais balais…). Valstybė susirūpinus, kad trūksta specialistų, IT, inžinierių. Aš atsiliepiu, štai, aš esu, mano gyvenimo hobis kompiuterija. Bet valstybė (tiksliau NEC) atsuka tau trijų pirštų kombinaciją. Mažiausiai vieniems metams man studijos kainuos… Vėliau gal pavyktų per rotaciją pereiti į nemokamą vietą. Ar neturėtų mokslas būt nemokamas to nusipelnusiems? Juk jie (neemigravę) dirba valstybei, moka mokesčius valstybei. Už galimybę uždirbti daugiau ir, SVARBIAUSIA, valstybės požiūriu, mokėti didesnius mokesčius valstybei aš turiu nemažai susimokėti, o tas nemažai, mano atveju, esančiam skurdžioje padėtyje, yra labai daug.
Aišku, jūs galite nesutikti su pastarąja mintimi, bet esmę supratote -- man net neleidžiama įrodyti jog esu gabus ir nusipelnęs finansavimo. Per neteisingą durnų ir gabių diferencijavimo sistemą aš patekau kaip tik į pirmąją grupę, nors neturėčiau ten būt… Mane uždeda etiketę, kad esu negabus, „nesugebėjau net valstybinio egzamino išlaikyt“… Absurdo teatras…
Pasimokyk, dar geriau įsidarbink kur už ačiū/už praktiką, pasidaryk portfeliuką ir varyk į užsienį kitais metais. Su portfeliuku/praktika laisvai gausi darbą ir išsilaikysi. Sėkmės. Valstybiniai egzai dar negyvenimo pabaiga. Mokslas daugumoje Europos šalių nemokamas, na aišku kalbą dar reikės išmokti, bet stengiantis metų turėtų pakakti. Arba pradėk LT, kad ir mokamą, tada bus perskirstymas neatsimenu po kiek metų, bus daug atkritusių „krepšelinių“ ir pereisi į nemokamą.
Mano visi draugai informatikai aiškina, kad diplomas nebūtinas, jei iš tiesų moki dirbti.