Vakar vienas pusprotis mano straipsnyje apie Būlio algebrą parašė komentarą apie tai, kad matematika (tiksliau, visiškai elementarūs skaičiavimai) yra šyvos kumelės briedas. Esmė tame, kad anas komentatorius net esuprato, ką jis skaičiuoja ir jam pasirodė, kad jei prie teigiamų n ir m pridėsi po teigiamą x, tai skirtumas tarp n ir m padidės.
Šiu atveju, kaip supratau, kalba net nebuvo apie aritmetinį skirtumą (vis dar darau prielaidą, kad tokio absurdiško durnumo žmonių čia pas mane neateina). Aritmetinis skirtumas išvis nesikeičia prie tokių sumavimų: (n-m)=(n+x)-(m+x), t.y., koks bebūtų x, jisai nepasikeis.
Kaip supratau, ano komentatoriaus nesuvokimas buvo apie tai, kad jei prie n ir m pridėsim po x, tai pasikeis santykis – t.y., jei n buvo mažiau už m, tai n pasidarys dar mažiau už m. Čia irgi absurdas, tiktai gal ne toks akivaizdus. Absurdiškumas pasimato tada, kai pabandai įsivaizduoti, kaip keisis santykis, keičiantis pajamoms. Gražiausiai tai matosi grafike:
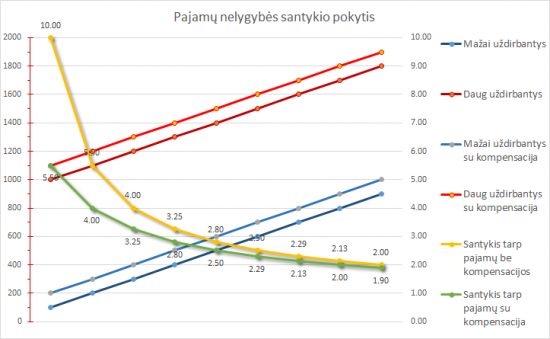
Kaip matome, kuo mažesnės pajamos, tuo labiau pasijunta kompensacijos dydis. Jei pajamos tėra 100 eurų, tai pridėjus 100 eurų kompensaciją ir 100, ir 1000 eurų uždirbantiems, pajamų nelygybė sumažėja kone du kartus – santykis pasikeičia iš 10 į 5,5.
Labai paprasta viską pamatyti, kai pabandai paskaičiuoti: vat tarkim, pas kažką gal pajamos 300 eurų ir valstybė, pvz., apmoka 100 eurų kainuojantį darželį. O pas kažką pajamos gal 1200 eurų, ir valstybė irgi duoda 100 eurų kompensacijos. Kaip pasikeičia santykis tarp pajamų? Ogi be kompensacijos tas santykis buvo 4 kartai, o su kompensacija pasidarė 3,25 karto, t.y., labai labai riebiai sumažėjo.
Aš suprantu, kur kažkam kirmėlės graužia – norisi, kad tie buržujai turčiai negautų jokių kompensacijų, nes jie ir taip turtingi. Bet reikalas tame, kad tiesiniai kompensavimo mechanizmai realiai suveikia kaip progresiniai. Ir net jei neduosi tam daug uždirbančiam kompensacijos, skirtumas pasikeis gana nežymiai: vietoje 3,25 karto bus tiesiog 3 kartai.
Tokie dalykai labai aiškiai pasimato, kai tiesiog pradedi skaičiuoti – nes matematika yra matematika ir viskas. Bet kol nebandai skaičiuoti, tai gaunasi visokie marazmai. O kai į matematiką žiūri kaip ožys į naujus vartus, tai pamatęs tokius skaičiavimus, gali nutarti, kad šitie skaičiavimai yra kažkoks šyvos kumelės briedas.
Deja, čia ne skaičiavimai yra briedas. Durniai yra tik tie, kurie pamatę akivaizdžius skaičius, ima sakyti, kad čia yra nesąmonės.
Beje, aš laikas nuo laiko vis atsimenu, kaip kartą prie straipsnio apie Ebolą ir jos plitimo tempus (tuo metu jie buvo nevaldomi) pas mane atėjo kažkokie humanitarai, kurie, kaip paskui paaiškėjo, net nesugebėjo sudėties nuo daugybos atskirti. Anie puskvaišiai dar paskui man mėtė kažkokias absurdiškas nuorodas, kurias rado, į Google įvedę kažkokius jiems patiems nesuprantamus žodžius. Tomis nuorodomis (nieko bendro netgi neturėjusiomis su tuo, ką jie bandė įrodinėti) jie man bandė įrodyti, kad eksponentinės sekos yra tiesinės 😀
Ponai ir ponios, netgi klaikiai nuobodi matematika būna labai labai įdomi. Bet jei tos klaikiai nuobodžios matematikos pagrindų nesimokai – paskui lieki durniaus vietoje, ir tada iš tavęs kas nors skaldo bajerius, o tu piktiniesi ir nesupranti, kodėl tave durniumi vadina.
Kiek nukrypstant – matematika yra labai įdomi, bet tai, kaip jos moko mokyklose – tai yra klaiku ir pasibaisėtina. Matematikos moko taip, kad ji būna baisesnė gal netgi ir už chemiją. Ir visai nenuostabu, kad beveik niekas jos neišmoksta, o tiktai iškala atmintinai.
Išties matematikos pagrindai nėra sudėtingi, jie yra netgi labai įdomūs ir naudingi, svarbu tik juos suprasti.









